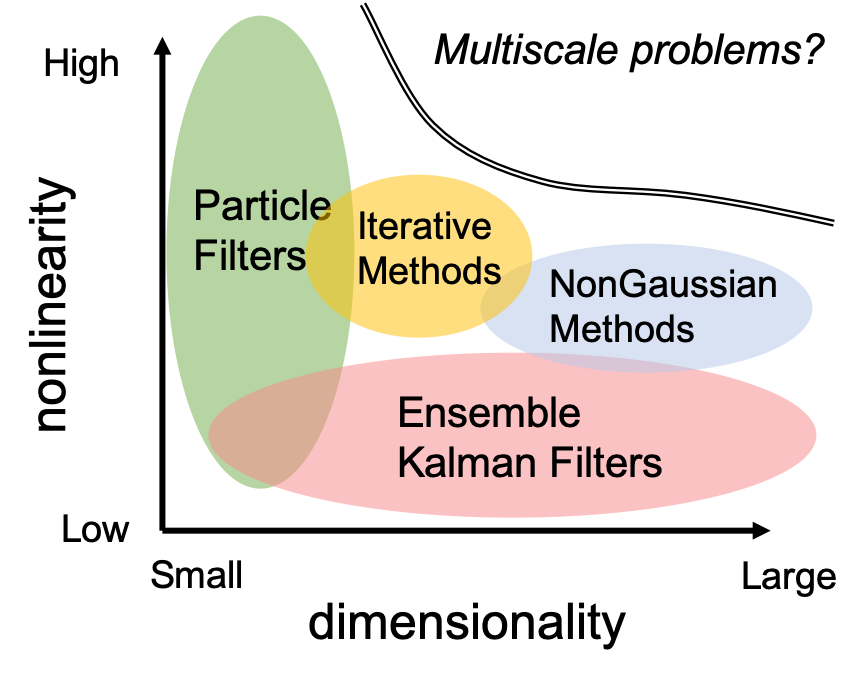
Ever-increasing complexity of multiscale dynamical systems poses challenges to data assimilation methods. Rapid error growth at small scales gives rise to nonlinearity, and multiscale systems typically have large dimensionality as well. Currently, methods based on linearization, such as the Ensemble Kalman Filter (EnKF), work efficiently for large problems but cannot handle high nonlinearity. On the other hand, nonlinear methods, such as the Particle Filter, are still not feasible for large dimensional problems. I have been developing new methods that can both handle nonlinearity and be efficient enough for the multiscale prediction problems.
Scale-dependent covariance localization
My first attempt was to reduce the dimensionality through localization. In Ying et al. 2018, we tested the scale dependency of best localization distances using a quasi-geostrophic model. The following figures show the correlation map between the observation "+" and the model state at each scale, and the circles show the best localization distances.
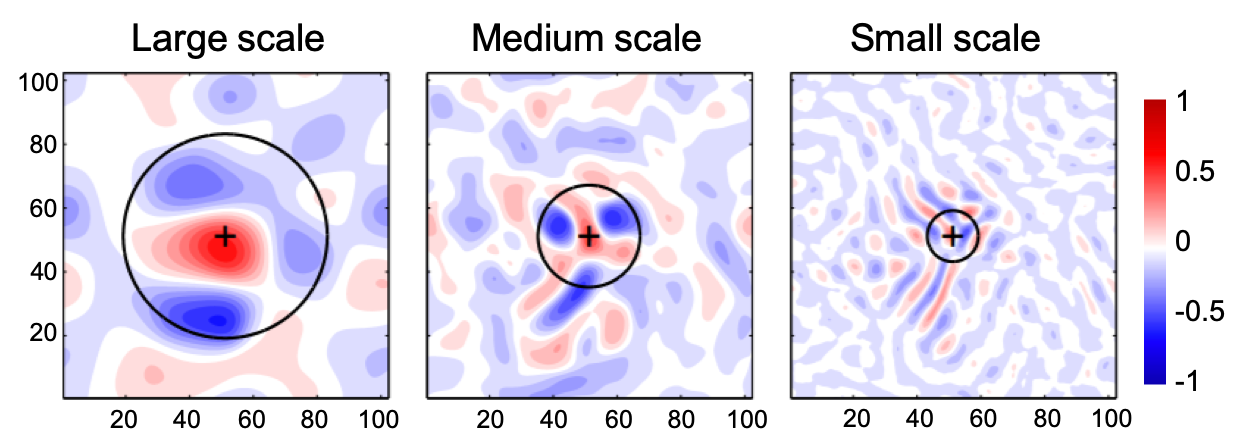
These results motivate a scale-aware data assimilation approach, where large- and small-scale components of the system can be treated separately.
Reducing displacement errors through "multiscale alignment"
I then noticed that displacement of coherent structures (position errors) is a major source of nonlinearity at small scales. The following figures show ensemble spaghetti plots of Rankine vortices before and after assimilating observations using EnKF. The ensemble members only differ in location of the vortex. As the location spread increases, the prior error distribution deviates more from a Gaussian, causing the EnKF analyses to be suboptimal.
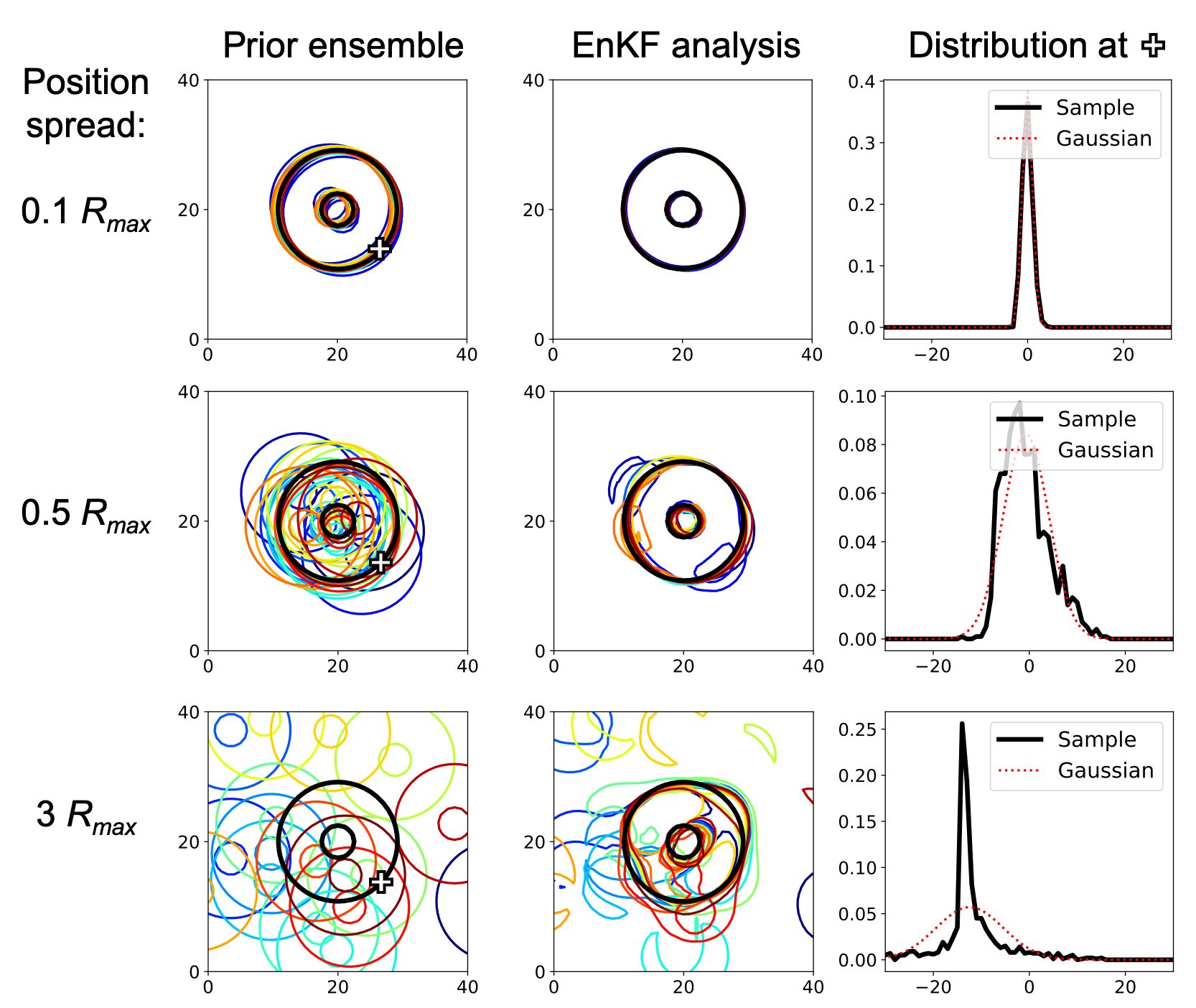
I was inspired by the computer vision literature on optical flows, and developed a "multiscale alignment" method that can successively reduce displacement errors from large to small scales of the system. The method is described in detail in Ying 2019 and I performed a proof of concept test with a two-layer quasi-geostrophic model.
Now, I am further developing the new method in more realistic and complex scenarios. The following figures show a sequence of surface zonal wind maps from large to small scales during one analysis cycle of Hurricane Patricia (2015).
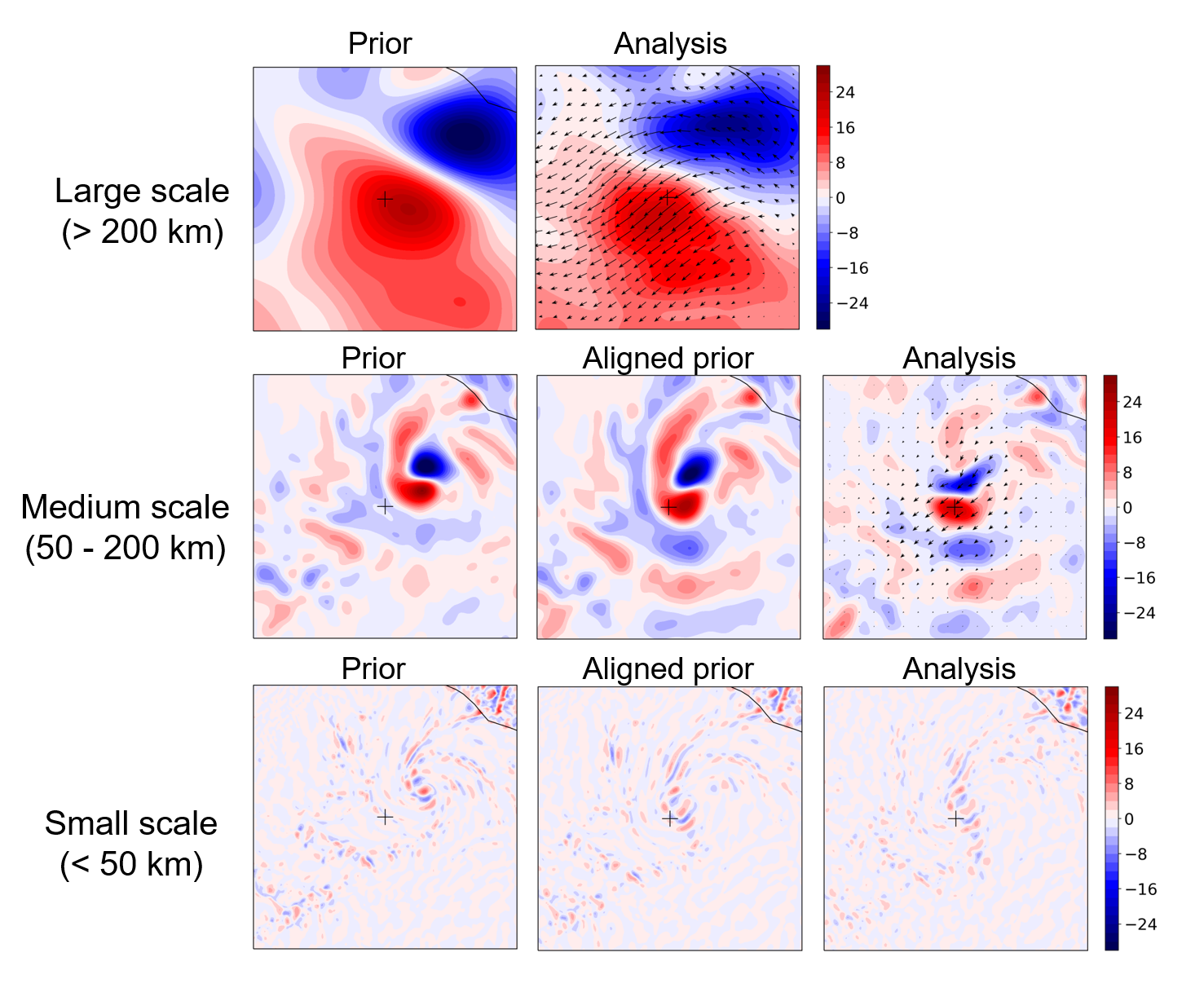
Displacement vectors are derived from the analysis increment from the assimilation at each scale, which are then used to warp the state at the subsequent smaller scales (to form the "aligned prior") before the observations are assimilated.
Adaptive algorithms to achieve the best use of observations
Tuning of parameters in a data assimilation system, such as covariance localization and inflation, is important for filter performance but also very time consuming. Adaptive methods that set the parameters automatically are favorable. To achieve the best use of observation information, the correct error covariances need to be specified for both the prior state and observations.
In Ying and Zhang 2015, we introduced an adaptive version of the relax-to-prior-spread (RTPS) covariance inflation method. This method can adapt to temporally and spatially varying observation density and quality. It is now adopted in the PSU_WRF_EnKF system, as well as by other data assimilation research groups.
Scale mismatch between the state and the observation give rise to representation errors that have non-zero spatial correlations. For a serial EnKF that assumes uncorrelated observation errors, tuning a fixed inflation factor cannot resolve this issue. A multiscale scheme that decompose the observations into scale components is proposed to allow the state/observation inflation to be tuned differently for each scale (Ying 2020).
Towards an integrated multiscale approach
Putting everything together, the workflow of the proposed multiscale approach can be shown as follows.
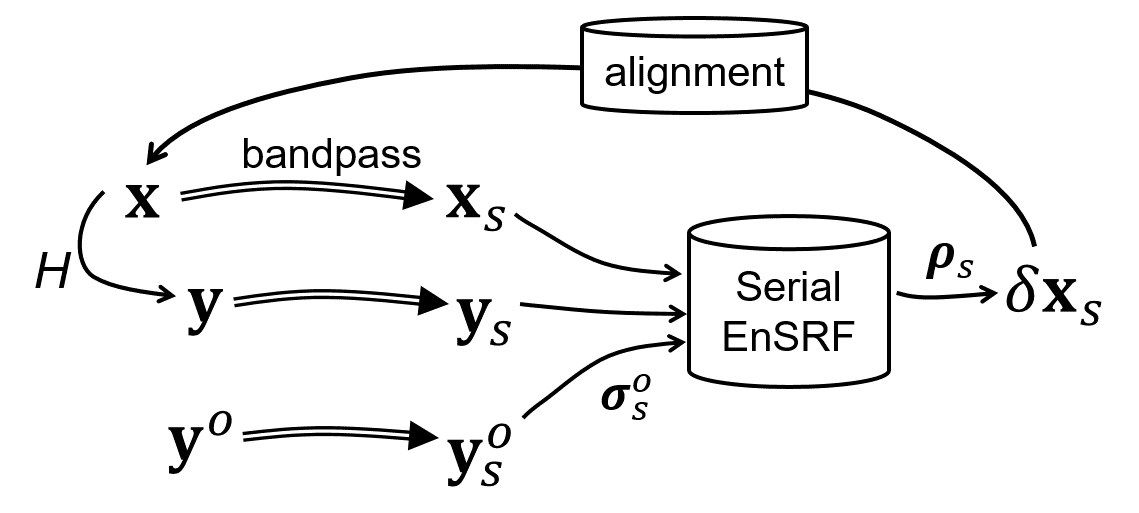
\(\mathbf{x}\) is the model state, \(\mathbf{y} = h(\mathbf{x})\) is the observation prior, and \(\mathbf{y}^o\) is the actual observation. The double-lined arrow is a bandpass filter that extracts a certain scale component indexed by \(s\). \(\delta\mathbf{x}\) is the analysis increment found by a core assimilation algorithm (serial EnSRF in this case). \(\sigma^o\) is the specified observation error std, and \(\boldsymbol{\rho}\) is the localization function. The multiscale approach processes large to small scale components sequentially (for \(s=1, 2, \ldots, N_s\)) and update the model state iteratively.
I am currently working on the implementation of such multiscale approach in the PSU_WRF_EnKF system and the DART system (on-going). If you are working on a problem where you think the multiscale data assimilation method might help, please don't hesitate to contact me!